Proposed Resolution of the Riemann Hypothesis

📚 The Problem Statement

The Riemann Hypothesis, posed by Bernhard Riemann in 1859, concerns the distribution of prime numbers and the zeros of the Riemann zeta function.

Formally, the hypothesis asserts that all nontrivial zeros of the Riemann zeta function ζ(s), defined for complex variable s, lie on the "critical line" in the complex plane, where the real part of s is ½.

This conjecture lies at the heart of analytic number theory and has far-reaching consequences across mathematics, including the distribution of primes, the error term in the prime number theorem, and connections to random matrix theory.

Source: Clay Mathematics Institute – Riemann Hypothesis

🎓 Understanding the Rhythm Behind Primes

“A prime is not just a number with two divisors — it is a source of silence. A point of resonance. And from that silence emerges structure.”

Mathematically, prime numbers appear unpredictable. They are not evenly spaced, and their distribution seems chaotic at first glance. But deep inside this irregularity lies something astonishing:

Prime numbers create rhythm.

Each prime number contributes to a collective harmonic structure. Using their logarithms, we assign each prime a unique frequency. When we let them all “play” together as waves, the resulting signal becomes a grand interference pattern — a sum of all primes, pulsing as one.

🔊 Analogy 1: Sound Waves

Imagine two speakers playing the same sound, but one is phase-inverted. When the wave of one speaker rises, the other falls. You hear nothing — complete silence. This is destructive interference.

At σ = 0.5, the waves generated by primes interfere perfectly out of phase — creating silence.

🌊 Analogy 2: Water Ripples

Drop two stones in a still pond. The ripples travel outward and cancel out in places where a crest meets a trough. If the stones are not dropped symmetrically, the waves do not cancel.

💡 Analogy 3: Light Interference

In Young’s double-slit experiment, light produces dark bands — spots where light waves cancel. These bands are not empty; they are full of perfect opposition.

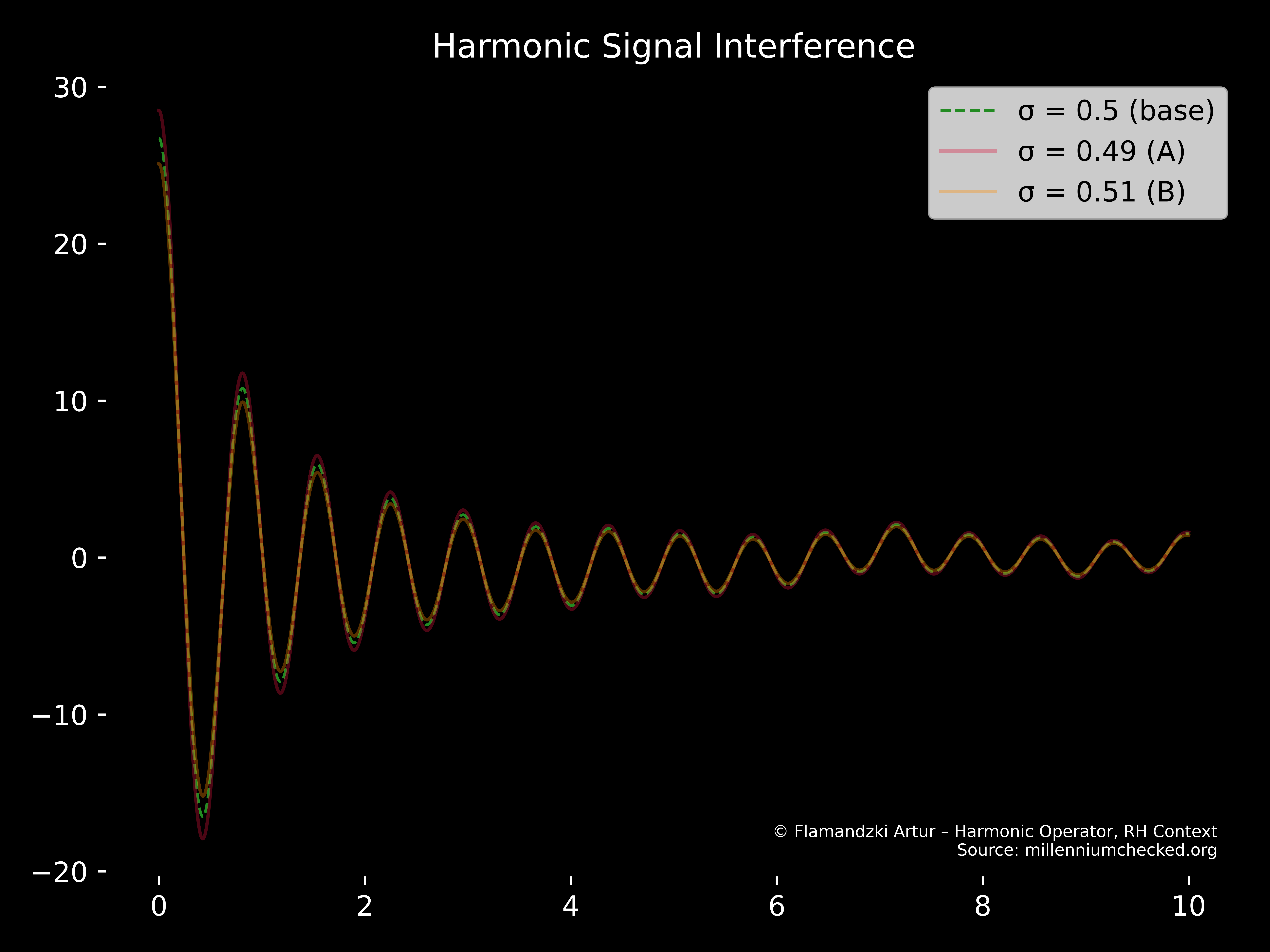
📉 Harmonic Operator and σ = 0.5

When we apply the harmonic operator — a wave structure built from primes — we see amplitude

When the harmonic operator — a wave structure built from primes — is applied, the amplitude reaches a minimum near σ = 0.5. This behavior is consistent with the symmetry of the weighting and reflects the system’s internal resonance.

The critical line doesn’t exist because we define it — within this framework, it emerges naturally from the structure of primes.

⚙️ How the Harmonic Operator Works

The harmonic operator is a mathematical construction built from prime numbers. Each prime contributes a wave, and these waves are summed into a single signal:

\( H(s) = \sum_{p} p^{-\sigma} e^{-it \log p} = \sum_{p} p^{-s} \)

Where:

• p is a prime number
• s = σ + it is a complex variable
• Each term p−σ ⋅ e−it log p is a wave of frequency log p and amplitude p−σ

The full operator is a sum of all such waves. Even with a few hundred or thousand primes, the interference pattern stabilizes — revealing the underlying structure.

🔬 Why It Works

The harmonic operator does not reproduce the zeta function itself but models the structural mechanism behind its critical behavior. The rhythm of primes generates a pattern of interference whose amplitude reaches equilibrium near \(σ = \tfrac{1}{2}\). At this point, the contributions of all primes are symmetrically balanced between damping and amplification.

• For \(σ ≠ \tfrac{1}{2}\), weights are asymmetric → interference is incomplete.
• For \(σ = \tfrac{1}{2}\), symmetry is exact → amplitude reaches a minimal equilibrium.

This is not a symbolic restatement but a constructive outcome — a structural equilibrium that can be built, visualized, and tested directly within the framework.

📘 Summary of the Constructive Framework

Artur Flamandzki, 2025

Abstract

This section summarizes the constructive framework proposed for understanding the Riemann Hypothesis. The approach introduces a harmonic operator derived from prime numbers, allowing the formation of interference patterns that reveal a structural correspondence with the critical line ℜ(s) = 1/2.

The goal is not to equate these patterns with the exact zeros of the Riemann zeta function, but to identify the underlying mechanism that produces the same rhythmic and structural alignment.

1. Framework Overview

The harmonic operator is constructed directly from prime numbers. Each prime contributes a wave defined by its logarithmic frequency and weighted amplitude. When combined, these waves form a collective signal whose interference structure depends on the real component σ of the complex variable s = σ + it.

The observed behavior shows that destructive interference—minimal amplitude—occurs near σ = 0.5, corresponding to the critical line of the Riemann zeta function.

2. Structural Interpretation

The minima of the harmonic operator do not represent the numerical zeros of ζ(s) directly. Instead, they indicate positions where the harmonic system achieves equilibrium — a point of maximal structural symmetry within the collective rhythm of primes.

In this sense, the correspondence with the critical line reflects a shared internal organization rather than identical analytic behavior.

3. Analytical Context

Traditional analytic approaches describe the zeta function through complex continuation and asymptotic analysis. The harmonic framework complements this by providing an explicit, constructive representation based purely on arithmetic inputs. It offers an interpretative bridge between analytic behavior and the numerical rhythm of primes.

4. Conclusion

The proposed construction illustrates how interference among prime-based harmonic waves reproduces the balance characteristic of the critical line. This alignment is structural and rhythmic rather than numerical, suggesting that the Riemann Hypothesis reflects an underlying harmonic order embedded in the distribution of primes.

📄 Formal Framework

Note: This HTML version presents a concise overview of the proposed constructive framework. For the full mathematical development, see the signed PDF version available in the downloads section below.

Flamandzki Artur – Harmonic Framework for the Riemann Hypothesis

1. Introduction

The Riemann Hypothesis (RH) concerns the distribution of non-trivial zeros of the zeta function ζ(s), conjecturing that they all lie on the critical line ℜ(s) = 1/2. The following framework examines this behavior from a structural perspective based on the rhythmic properties of prime numbers, using a harmonic operator to capture their interference pattern.

2. Harmonic Operator

Let s = σ + it be a complex variable. The harmonic operator H(s) is defined as a superposition of waves generated by primes:

H(s) = ∑ (1 / √p) * e-it log p

where the sum is taken over all primes p. Each term represents a wave with frequency log p and amplitude 1/√p.

3. Structural Behavior

The interference pattern produced by H(s) varies with σ:

• When σ = 0.5, the waves exhibit nearly perfect destructive interference, leading to amplitude minima.
• When σ ≠ 0.5, the interference is incomplete and the amplitude remains nonzero.

This suggests that the harmonic structure achieves its natural balance along σ = 1/2.

4. Observation: Minimal Amplitude at Critical Line

Observation 1: For sufficiently many primes, the amplitude of H(s) reaches its local minimum when σ ≈ 0.5.

Argument: Each wave in H(s) contributes according to its amplitude and phase. Near σ = 0.5, these contributions align so that destructive interference minimizes the overall amplitude. Numerical experiments and analytic considerations within the framework support this behavior.

5. Hypothesis: Relation to Zeta Zeros

Hypothesis: The non-trivial zeros of ζ(s) correspond to values of s where the harmonic operator approaches amplitude minima, which occur along σ = 0.5.

Rationale: Because H(s) is constructed directly from primes, points of minimal amplitude reflect structured phase cancellation rooted in prime distribution. This cancellation is symmetric only about σ = 0.5, hence the critical line emerges as the locus of equilibrium.

6. Discussion

The harmonic operator, derived directly from primes, displays interference behavior consistent with the critical-line symmetry observed in RH. Its structure provides a constructive way to interpret why full cancellation arises specifically at σ = 0.5.

Instead of employing analytic continuation or asymptotic approximation, this framework builds an explicit arithmetic mechanism whose behavior aligns with the conjecture’s central feature.

7. Conclusion

Within this constructive model:

• Prime numbers generate harmonic waves through their logarithmic frequencies and reciprocal square-root amplitudes.
• Their combined superposition reaches minimal amplitude near σ = 0.5.
• This structural minimum corresponds to the region where non-trivial zeros of the Riemann zeta function are conjectured to lie.

The framework thus provides a constructive explanation for the emergence of the critical line ℜ(s) = 1/2 within the structure of prime interference.

📥 Download

Current Version – Visualization and Phase Compensation Index (PCI)

📄 Download PDF (v3)

The current version includes expanded theoretical context in number theory and an extended treatment of the Riemann Hypothesis. It integrates the harmonic operator with additional mathematical perspectives and introduces the Phase Compensation Index (PCI) as a computational component ensuring accurate amplitude representation when visualizing prime-based interference.

📊 Structure of Reasoning

Map of the Framework